Есть БД со списком GPS-координат движения объекта. В Яндекс.Карты API строить кривую по координатам можно на основе не более 100 точек. Чтоб хоть немного обойти ограничение - хочу исключить точки, находящиеся на одной прямой. Собственно вопрос как вычислить, что между точками А и В, Б-точка также на прямой, либо нет? Я вижу решение в:
- рассчитать расстояния между А и Б, и между Б и В;
- рассчитать расстояние между А и В;
- если АБ + БВ = АВ (+/- погрешность), то это прямая, и точку Б можно исключить из кривой.
Как рассчитать расстояние между двух точек по GPS-координатам (например: А = 40.023568,53.782569; Б = 40.023789,53782956)? Координаты взяты для примера.
Или каким еще способом (с объяснением способа расчета) определить принадлежность трех точек - одной прямой, с некоторой погрешностью?
Спасибо!
Добавлено спустя 1 минуту 28 секунд:
Чуть не забыл. Высоту точки над уровнем моря можно игнорировать, т.к. расстояния между точек очень малы.
GPS - как узнать, все-ли точки на прямой?
Модератор: Модераторы
Классика.
1. Получив уравнение прямой, проходящей через две точки, подставьте значения координат третьей точки в него вместо переменных х и у. Если равенство получилось верное, значит все три точки лежат на одной прямой. Точно так же можете проверять принадлежность этой прямой других точек.
2. Проверьте принадлежность всех точек прямой, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли верным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.
3. Еще один способ проверить принадлежность трех точек прямой – посчитайте площадь треугольника, который они образуют. Если все точки лежат на прямой, то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если после всех вычислений вы получили ноль - значит, три точки лежат на одной прямой.
1. Получив уравнение прямой, проходящей через две точки, подставьте значения координат третьей точки в него вместо переменных х и у. Если равенство получилось верное, значит все три точки лежат на одной прямой. Точно так же можете проверять принадлежность этой прямой других точек.
2. Проверьте принадлежность всех точек прямой, проверив равенство тангенсов углов наклона соединяющих их отрезков. Для этого проверьте, будет ли верным равенство (х2-х1)/(х3-х1)=(у2-у1)/(у3-у1)=(z2-z1)/(z3-z1). Если один из знаменателей равен нулю, то для принадлежности всех точек одной прямой должно выполняться условие х2-х1=х3-х1, у2-у1=у3-у1, z2-z1=z3-z1.
3. Еще один способ проверить принадлежность трех точек прямой – посчитайте площадь треугольника, который они образуют. Если все точки лежат на прямой, то его площадь будет равна нулю. Подставьте значения координат в формулу: S=1/2((х1-х3)(у2-у3)-(х2-х3)(у1-у3)). Если после всех вычислений вы получили ноль - значит, три точки лежат на одной прямой.
sign, тут же не декартовы координаты, а широта и долгота.
2 sign - спасибо за формулы.
С площадями и углами не совсем удобно получилось Если все точки лежат на одной прямой, то нет возможности узнать крайнюю при начале движения в обратную сторону без дополнительных проверок. Все же с расчетом расстояний получается точнее.
Если все точки лежат на одной прямой, то нет возможности узнать крайнюю при начале движения в обратную сторону без дополнительных проверок. Все же с расчетом расстояний получается точнее.
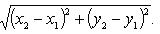
Добавлено спустя 3 минуты 15 секунд:
Это не имеет принципиальной разницы. Главное рассчитать разницу, и сравнить с допустимой погрешностью.
С площадями и углами не совсем удобно получилось
Добавлено спустя 3 минуты 15 секунд:
Дож писал(а):sign, тут же не декартовы координаты, а широта и долгота.
Это не имеет принципиальной разницы. Главное рассчитать разницу, и сравнить с допустимой погрешностью.
