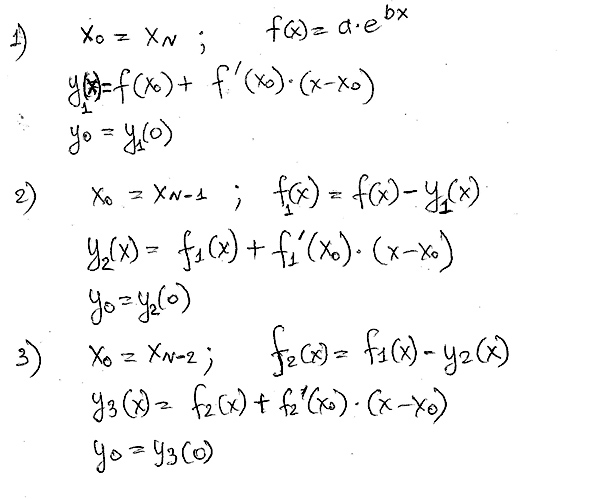Действия над функциями

[Mavlyudov]

Столкнулся с такой проблемой: надо запрограммировать действия над несколькими функциями.
Пробовал делать через передачу параметрова переменнй типа функции, но не получилось.
Сам алгоритм такой: есть некоторая функция y1(x). Далее записываем уравнение касательной y1(x) к ней в точке x0=x[n],
далее получаем функцию y2(x) как разность y1(x) и yk1(x) и получаем уравнение касательной в точке x0=x[n-1] и т.д.
по всем точкам из массива x.

Итерация 1
x0=x[n]
y1(x)=a*exp(b*x)
yk1(x)=y1(x0)+(dy1(x0)/dx)*(x-x0)
y0=yk1(0)

Итерация 1
x0=x[n-1]
y2(x)=y1(x)-yk1(x)
yk2(x)=y2(x0)+(dy2(x0)/dx)*(x-x0)
y0=yk2(0)

Итерация 1
x0=x[n-2]
y3(x)=y2(x)-yk2(x)
.................

dy1(x0)/dx - значение производной функции y1(x) в точке x0

[grot]

Попробуйте (Надо) быть проще:

1. в функцию передавать параметр
2. получить результат работы функции
3. проводить дальнейший расчет уже с этим результатом .

и повторить это сколько надо...

[Mavlyudov]

Не получается так

[Mavlyudov]

Вот код

Код: Выделить всё

type
tfunc=function(x:single):single;
tfunc2=function(x,x0,eps:single):single;
tfunc3=function(x,x0,eps:single;fp:tfunc2):single;
tfunc4=function(x,x0,eps:single;fp1:tfunc2;fp2:tfunc3):single;

function dfdx(x0,eps:single;f:tfunc4):single;
var
dx,dy,dy2:single;
fz2:tfunc2;
fz3:tfunc3;
begin
dx:=1;
repeat
dx:=dx/2;
dy:=f(x0+dx/2,x0,eps,fz2,fz3)-F(x0-dx/2,x0,eps,fz2,fz3);
dy2:=F(5*x0/4+dx,x0,eps,fz2,fz3)-2*F(5*x0/4,x0,eps,fz2,fz3);
dy2:=dy2+F(5*x0/4-dx,x0,eps,fz2,fz3);
until abs(dy2*dy2*F(x0,x0,eps,fz2,fz3)/(2*dx))<eps;
dfdx:=dy/dx;
end;

function yn(x,x0,eps:single;fp1:tfunc2;fp2:tfunc3){(x:single)}:single;
begin
yn:=146.60715*exp(-0.18192*x);
end;

function ykn(x,x0,eps:single;fp1:tfunc4):single;
var
fz2:tfunc2;
fz3:tfunc3;
begin
ykn:=fp1(x0,x0,eps,fz2,fz3)+dfdx(x0,eps,fp1)*(x-x0);
end;

function fdif(x,x0,eps:single;fp1:tfunc2;fp2:tfunc3):single;
begin
fdif:=fp1(x,x0,eps)-fp2(x,x0,eps,fp1);;
end;

var
f1,f2:text;
i,n,j:integer;
xt,yt,EPP,MPP:array[1..100] of single;
k1,eps1,eps2,x0,y0:single;

y1:tfunc4;
fp3:tfunc3;
fp2:tfunc2;

begin
//for j:=1 to n do begin
//x0:=xt[n-(j-1)];
{Итерация 1}
x0:=xt[n];
y1:=yn;
y0:=ykn(0,x0,eps1,y1); {!}

{Итерация 2}
x0:=xt[n-1];
y1:=fdif; {!}
y0:=ykn(0,x0,eps1,y1);

//end;{j}
readln;
end.

Во второй итерации идёт присвоении функции без передачи ей параметров. Не знаю, как передать

[Alex2013]

Не совсем понял зачем тут обязательно нужен "тип функции"
Но я иногда что-то подобное делаю чрез указатели и преобразование типа
То есть примерно так:

Код: Выделить всё

type 
tfunc=function(x:single):single;

function R_F(x:single):single;
begin
R_F:=Sin(X)*x;
end;
Var  
F:tfunc;
Y,X:single;
begin
X:=1;
F:=tfunc(@R_F);
Y:=F(X);
Writeln('Y=',y);
end.

По крайней мере так точно компилируется...
(возможно что @ тут излишняя но хуже от нее не будет )

[Mavlyudov]

Alex2013
У меня вроде тоже самое сделано.
Ну а без процедурного типа не понимаю как сделать. Если знаешь, напиши как

[Alex2013]

Alex2013
У меня вроде тоже самое сделано.
Ну а без процедурного типа не понимаю как сделать. Если знаешь, напиши как

не тоже ...
Сделано так y1:=fdif; а нужно y1:=tfunc4 (@fdif); то есть нет "привидения типа".
Зы
Вникать в алгоритм если честно лень, но без приведения типа этот код вообще компилироваться не должен. ( разве что "дельфи моде" и то сомневаюсь )
И еще процедурная/функциональная переменная в параметрах малость моветон . ( нужно проверять состояние и вообще делая итерации таким образом код можно запросто "закольцевать " ("кольцевание" это наиболее жестокий и часто очень неявный случай зацикливания ) )
Зы
Как сделать без ф-переменной ? Например можно предавать в процедуру флаг и вызвать нужную функцию по case .
Зы Зы
И еще например ...

Код: Выделить всё

function ykn(x,x0,eps:single;fp1:tfunc4):single;
var
fz2:tfunc2;
fz3:tfunc3;
begin
ykn:=fp1(x0,x0,eps,fz2,fz3)+dfdx(x0,eps,fp1)*(x-x0);
end;

Откуда ( и зачем) локальные fz2:tfunc2; fz3:tfunc3;? С потолка ? Там-же "страшный Nil" живет . и т.д. и т.п.

[Mavlyudov]

Сделано так y1:=fdif; а нужно y1:=tfunc4 (@fdif); то есть нет "привидения типа".

Тут смысл в том, чтобы присвоить функции функцию и передать ей параметры.
Компилирует только так

Код: Выделить всё

y1:=tfunc4(@fdif);

А по идее надо вот так:

Код: Выделить всё

y1:=tfunc4(@fdif(x,x0,eps1,fp1,fp2)); 

Ругается на параметр x, что не удивительно. Но его я не могу передать.

Вникать в алгоритм если честно лень, но без приведения типа этот код вообще компилироваться не должен. ( разве что "дельфи моде" и то сомневаюсь )

Да тут и алгоритма нет: в первом посте я описал его.

[Снег Север]

Честно говоря, не смог врубиться в суть проблемы - сотни раз пользовался процедурными переменными и никаких проблем не встречал (если делать правильно, по документации). В некотором общем модуле или фрагменте кода, включаемом по команде $I, описывается тип функциональной переменной, а потом можно сколько угодно создавать переменные этого типа и им присваивать конкретные экземпляры функций.
Проблемы могут возникнуть только при попытках грязных хаков или использовании безграмотно портированных сишных функций из длл.

[Alex2013]

y1:=tfunc4(@fdif(x,x0,eps1,fp1,fp2));

Дико извиняюсь, но это бред ...
var
F:single;
y1:tfunc4;
/..
y1:=tfunc4(@fdif); ///это присвоение адреса реальной функции функциональной переменной
F:=Y1 (x,x0,eps1,fp1,fp2); //это вызов САМОЙ функции.
Зы
Вообщем боюсь что возможно просто нет понимания как работают обычные функции, а использование функциональной переменной и функционального типа вообще "увеличение сущностей сверх необходимого" (с)Старик О`Кам.

[Mavlyudov]

Alex2013
Помоги тогда поправить

[Alex2013]

Alex2013
Помоги тогда поправить

Проблема в том что я не понял самой задачи .
(и судя по другим отзывам видимо не понял не только я )
Но приведенный код явно изобилует ошибками .
С ошибками я могу помочь но смысла в этом мало .
(Я уже пытался)

[delphius]

Код: Выделить всё

program TangentApproximation;

uses Math; // Для использования exp и других математических функций

const
  n = 3;  // Число точек
  a = 1.0;
  b = 0.5;

type
  TArray = array[1..n] of real;

var
  x: TArray = (1.0, 2.0, 3.0); // Массив точек
  i: integer;
  yk, yk_prev: real;

// Функция y1(x) = a * exp(b * x)
function y1(x: real): real;
begin
  y1 := a * exp(b * x);
end;

// Производная dy1(x)/dx = a * b * exp(b * x)
function dy1(x: real): real;
begin
  dy1 := a * b * exp(b * x);
end;

// Функция y(x) для итераций: y2(x), y3(x), ..., вычитая предыдущие касательные
function y_diff(x: real; yk_prev: real; x0: real): real;
begin
  y_diff := y1(x) - yk_prev;
end;

// Функция касательной к y(x) в точке x0
function tangent_line(x: real; x0: real; dy_dx: real): real;
begin
  tangent_line := y1(x0) + dy_dx * (x - x0);
end;

begin
  writeln('Итерационный процесс:');
  yk_prev := 0.0;  // Начальное значение касательной
  for i := n downto 1 do
  begin
    // x0 = x[i], расчет касательной
    yk := tangent_line(0, x[i], dy1(x[i]));  // Вычисляем yk в точке x[i]

    writeln('Итерация ', n - i + 1, ':');
    writeln('x0 = ', x[i]:4:2);
    writeln('Касательная yk(x) в точке x0 = ', x[i]:4:2, ' равна ', yk:8:4);
    writeln('Производная в x0: dy1(x0)/dx = ', dy1(x[i]):8:4);

    // Вычисляем разницу функции y_diff
    if i > 1 then
    begin
      yk_prev := tangent_line(0, x[i-1], dy1(x[i-1]));  // Касательная для следующей итерации
      writeln('y0 на следующем шаге = ', yk_prev:8:4);
    end;

    writeln;
  end;

  readln;
end.

[Alex2013]

Ну вот что я и говорил . (delphius молодец взял на себя труд вникнуть в "оригами-код" или что более вероятно в описание задачи в начале темы, но вообще при такой "постановке задачи" помочь трудновато, дело в том что "псевдокод" в описании вещь иногда полезная, но обращаться с ним нужно аккуратно иначе вместо помощи в понимании алгоритма он тупо вызывает мигрень при попытке сходу в него вникнуть )

[Mavlyudov]

delphius
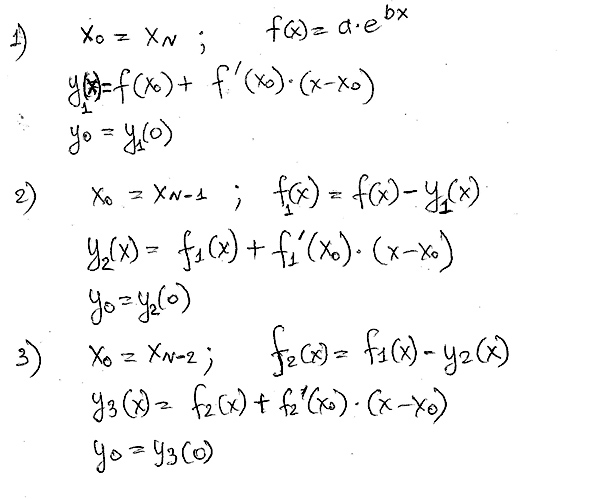
Возможно, я где-то не так написал, но производная должна браться от каждой новой функции.