Страница 2 из 3
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:17:18
vitaly_l
vada писал(а):Осталось то всего-ничего - понять где кончается прямая, а начинается кривая. Мелочи
)))))))))))))) Да! Именно это, сейчас и пытаюсь понять, чтобы сделать в виде алгоритма.
Вот из какого-то примера на Си честно стырил. С помощью неё можно, найти мне кажется.
Код: Выделить всё
// Вычисление коэффициентов аппроксимирующей прямой
void getApprox(double **x, double *a, double *b, int n) {
double sumx = 0;
double sumy = 0;
double sumx2 = 0;
double sumxy = 0;
for (int i = 0; i<n; i++) {
sumx += x[0][i];
sumy += x[1][i];
sumx2 += x[0][i] * x[0][i];
sumxy += x[0][i] * x[1][i];
}
*a = (n*sumxy - (sumx*sumy)) / (n*sumx2 - sumx*sumx);
*b = (sumy - *a*sumx) / n;
return;
}
https://prog-cpp.ru/mnk/
мат. формула: http://mathhelpplanet.com/viewtopic.php?f=37&t=630
//сплайн по четырем координатам
private void drawSpline(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4,
Pen pen)
{
//подсчет коэффициентов сплайна
float a0 = countSplineCoefficient(0, x1, x2, x3, x4);
float a1 = countSplineCoefficient(1, x1, x2, x3, x4);
float a2 = countSplineCoefficient(2, x1, x2, x3, x4);
float a3 = countSplineCoefficient(3, x1, x2, x3, x4);
float b0 = countSplineCoefficient(0, y1, y2, y3, y4);
float b1 = countSplineCoefficient(1, y1, y2, y3, y4);
float b2 = countSplineCoefficient(2, y1, y2, y3, y4);
float b3 = countSplineCoefficient(3, y1, y2, y3, y4);
float xPrev = a0, yPrev = b0;
for (int i = 1; i <= 20; i++) //разбиваем кривую на 20 отрезков
{
float t = i / 20.0f;
float x = ((a3 * t + a2) * t + a1) * t + a0; //x(t)
float y = ((b3 * t + b2) * t + b1) * t + b0; //y(t)
g.DrawLine(pen, xPrev, yPrev, x, y); //соединяем подсчитанные точки
xPrev = x;
yPrev = y;
}
}
//пересчет коэффициентов сплайна
private float countSplineCoefficient(int index, int x1, int x2, int x3, int x4)
{
switch (index)
{
case 0:
return (x1 + 4 * x2 + x3) / 6.0f; //свободный член
case 1:
return (-x1 + x3) / 2.0f; //коэффициент при t
case 2:
return (x1 - 2 * x2 + x3) / 2.0f; //коэффициент при t^2
case 3:
return (-x1 + 3 * x2 - 3 * x3 + x4) / 6.0f; //коэффициент при t^3
}
return 0;
}
http://grafika.me/node/458
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:33:02
Лекс Айрин
vitaly_l писал(а):Именно это, сейчас и пытаюсь понять, чтобы сделать в виде алгоритма.
Продолжаешь прямую, пока есть возможность, пытаешься провести кривую с запасом... примерно посередине совпадающего отрезка и ставишь точку смены кривой/прямой и соответствующим образом отрисовываешь сегменты.
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:36:38
vitaly_l
Лекс Айрин писал(а):Продолжаешь прямую, пока есть возможность
на словах просто, а на пикселях. это несколько сложнее, т.к. тогда вначале нужно было бы вычислить функцию прямой.
А с кривой... там вообще, засада. Одно дело нарисовать Cathmull-Rom, а вот вычислить из точек...

Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:36:49
zub
vitaly_l
Лекс Айрин
Флеймисты - оптимисты
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:40:09
vitaly_l
zub писал(а):Флеймисты - оптимисты
Зуууб-ик... Так Вы знаете формулу? Типа знаю но не скажу? ага....
Вот смотрите: Была такая притча, там умная ворона, сыр во рту держала. Держала, держала.. Держала, держала.. А тут глупая лиса подходит и говорит:
zub, а самому что, слабо посчитать и показать результат в коде?
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:43:00
zub
Стряпайте сами, у меня пирожков нет))
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:44:15
Лекс Айрин
zub, я лишь предложил))))
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 17:44:35
vitaly_l
zub писал(а):Стряпайте сами, у меня пирожков нет))
И ангельский должно быть это код?
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 18:02:14
Лекс Айрин
vitaly_l, идеальным код бывает редко.
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 18:03:15
Pavia
А смысл озвучивать формулу если ТЗ до сих пор вилами по воде писано?
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 18:06:00
vitaly_l
Pavia писал(а):А смысл озвучивать формулу если ТЗ до сих пор вилами по воде писано?
А вдруг эта Ваша формула тоже кому-то пригодится? Народу на форум заходит много.... формула одна...
Так значит вкусный сыр у Вас?
.
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 18:38:03
Pavia
Почему одна? Я знаю кучу формул. А в задаче выделения контуров каждый год появляются новые формулы. Вот к примеру рейтинг
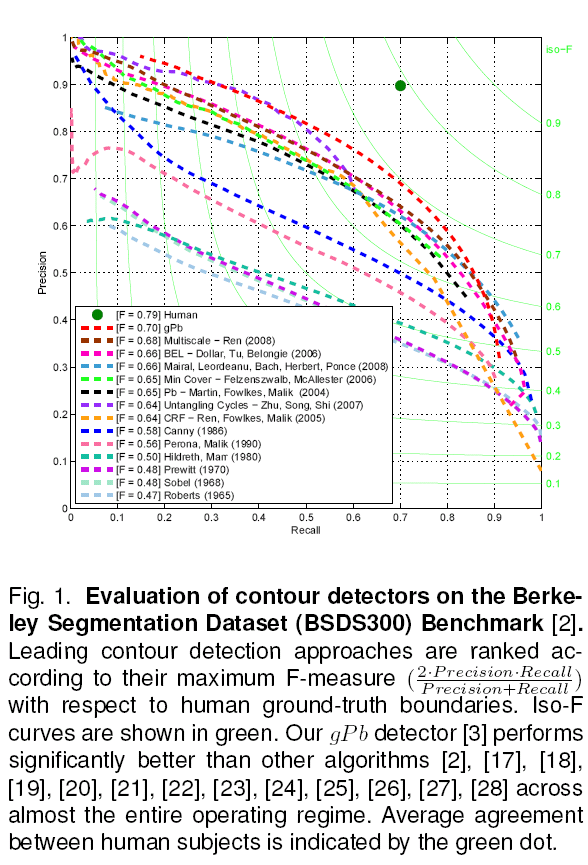
Картинка кликабельна.
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 18:55:35
vitaly_l
Pavia писал(а):А в задаче выделения контуров каждый год появляются новые формулы
Я не решаю задачу выделения контуров или их detection. Мне нужно сделать векторную аппроксимацию контура. Например буква P состоит из 111 точек. А мне нужно сделать аппроксимацию, чтобы осталось всего только три точки и две линии (одна из которых Безье = Cathmull-Rom).
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 19:01:33
Pavia
vitaly_l писал(а):Я не решаю задачу выделения контуров. Мне нужно сделать векторную аппроксимацию контура. Например буква P состоит из 111 точек. А мне нужно сделать аппроксимацию, чтобы осталось всего только три точки и две линии (одна из которых Безье).
Эти задачи имеют много общего. Во-вторых кривизна кривой Безье не позволяет точно описать букву «Р». Тут как минимум надо 3 штуки этих кривых. Хотя если точностью пожертвовать, то можно и одну оставить.
Re: Апроксимация рисованной линии, при переводе в вектор.
Добавлено: 02.06.2017 19:04:10
Лекс Айрин
vitaly_l писал(а):чтобы осталось всего только три точки и две линии (одна из которых Безье = Cathmull-Rom).
Вообще-то в букве "Р" пять точек, три прямых линии и одна полуокружность. Если, конечно, считать ее линии однопиксельными.
